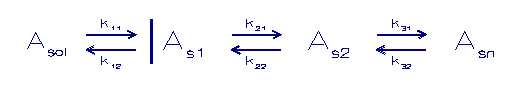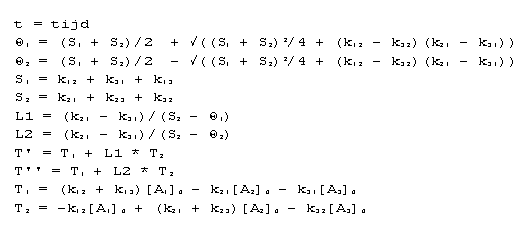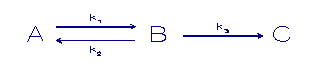5. Kinetische beschrijving van het
sorptie gedrag.
5.1. Inleiding
Sorptie proeven worden vaak uitgevoerd met als doel de
bestudering van het gedrag van een bepaalde component met een
bepaalde concentratie met een bepaald suspensie gehalte op
vastgestelde pH waarden. Daarbij blijkt de sorptie ook een
funktie van de tijd te zijn. De kinetiek van deze reacties
speelt een rol van betekenis. Beschrijving van deze kinetiek
kan daarom van belang zijn. Er is getracht om een kinetische
theorie te testen op de sorptie experimenten. Dit theoretische
model moet een hoge mate van betrouwbaarheid bezitten om het
gedrag van bv. een zwaar metaal in een suspensie te kunnen
bepalen. Een hoge mate van betrouwbaarheid kan bereikt worden
indien we het substraat voor 100 % zouden kennen.
Dit laatste is echter praktisch nooit het geval. De
experimenten die in het kader van dit onderzoek uitgevoerd
zijn werden
niet als specifiek kinetische experimenten opgezet. Ook werden
er maar in relatief beperkte mate sorptie proeven uitgevoerd
die als zodanig niet tot doel hadden kinetische studies te
verrichten.
5.2. Materialen en methoden
In het algemeen zijn sorptietoestanden dynamische
evenwichtstoestanden waar geen verandering optreedt indien het
medium
constant blijft. Indien een concentratie gradiënt
toegevoegd
wordt aan een medium kan men sorptie verklaren door kinetische
modellen. Deze kan men vaak analytisch of numeriek oplossen.
In ons geval werd o.a. gebruik gemaakt van analytische
oplossingen met het niet-lineaire programma van Systat
(Wilkinson,
1988) en van een modelleringsprogramma Frame. Het grootste
voordeel hierbij blijkt dat in het laatste programma de
differentiaalvergelijkingen ingevoerd konden worden zonder dat
men zich hoeft te bekommeren om de analytische oplossing. (Het
programma is als zodanig toegevoegd en is eenvoudig te leren.)
5.3. Resultaten en discussie
5.3.1. Theoretische modellen
Kinetische modellen kunnen een theoretische beschrijving geven
van het sorptiegedrag. Men kan dan met enkele parameters het
sorptiegedrag beschrijven. Dit betekent niet dat de
werkelijkheid er als zodanig uitziet, maar dat hij wel als een
deel
volgens een model verklaard kan worden. Via simpele modellen
kan een deel van het sorptie gedrag van metalen verklaard
worden.
In een natuurlijk systeem is er dynamische evenwicht tussen
verschillende fasen . Zo is het mogelijk dat er een snelle
adsorptie van een ion optreedt aan het oppervlak van het
substraat, gevolgd door een lanzame diffusie/adsorptie naar
energetisch voordelige plaatsen in het substraat.
Dit kan voorgesteld worden al een opeenvolgende sorptie
reactie.
In onderstaand schema wordt een component Asol welke in
oplossing is doorgegeven naar andere fasen. Dit verloopt
volgens
opeenvolgende eerste orde sorptiereacties. De componenten As1
tot Asn stellen verschillende vast fasen voor waar de
component
A zich over verdelen kan.
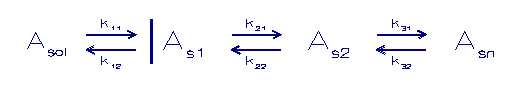
Asol = component A in oplossing
As1 - Asn = componenten A in de vaste fase
k = sorptie snelheidconstanten tussen de verschillende fasen
In onze adsorptie experimenten is alleen de opgeloste
concentratie bekend. Dit betekent dat we alleen een
verdwijning
kunnen waarnemen. Mochten er enige tussenfasen in de adsorptie
proces optreden dan kunnen we deze niet als zodanig
identificeren en kunnen dus niet bijdragen tot een betere
definiëring van van het model. Deze onbekendheid van
bepaalde
tussenfasen draagt bij tot onzekerheden van modellen.
Voor sorptie aan het oppervlak worden een aantal modellen
geïntroduceerd die de resultaten kunnen beschrijven. Een
complex systeem zal veel k-waardes hebben maar zal weinig
zekerheid geven m.b.t. zijn evenwichtsconstantes. Daarom werd
een systeem ontwikkeld met zo min mogelijk k-waardes.
In eerste instantie kan men denken aan een eenvoudige eerste
orde kinetiek.
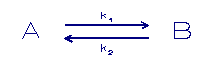
A = component in fase A
B = component in fase B
k = sorptie snelheidconstanten
Het bovenstaande sorptie verloopt met via een reversibele
eerste orde reactie. Dit betekent een exponentiële afname
van
de opgeloste concentratie totdat er een evenwicht ontstaat.
Een andere orde kinetiek is onwaarschijnlijk omdat men dan te
maken heeft met een continue afname in de opgeloste fase
totdat de opgeloste fase verdwenen is . Onderstaand model
geeft dit aan.

A = component in oplossing
B = component in een vaste fase
k = sorptie snelheidconstante
Dit zal onder natuurlijke omstandigheden niet optreden en
betekent dat alles adsorbeert.
Het is mogelijk dat een groot deel van de waarnemingen door
een eerste orde model verklaart kan worden vooral bij de start
van de adsorptie.
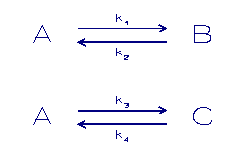
In volgend model doet een derde fase mee.

A = component in oplossing
B,C = component in een vaste fase
k = sorptie snelheidconstante
Het eerste evenwicht zal zich redelijk snel instellen, terwijl
een overdracht naar een volgende vaste fase minder snel zal
optreden.
Het eerste evenwicht wordt met de adsorptie snelheidsconste k1
en k2 zal snel optreden, gevolgd door een naar het binnenste
deel van het substraat sterker gebonden fasen. Dit laatste
proces wordt hier als irreversibel gesteld en wordt
gecontroleerd door de adsorptie (diffusie) snelheids
constante k3.
Een uitbreiding van dit model is de volgende:

A = component in oplossing
B,C = component in een vaste fase
k = sorptie snelheidconstanten
In dit laatste model is een reversibele stap ingebouwd tussen
de laatste 2 fasen dit betekent dat het systeem naar een
evenwicht gaat als de tijd toeneemt.
Het is mogelijk om dit systeem uit te breiden naar een verder
doorgeefmodel maar dit zal practisch weinig opleveren omdat
het systeem dan gecontroleerd wordt door 5 of meer parameters
zodat het geheel heel elastisch wordt en nauwelijks enige
voorspellende waarde meer heeft.
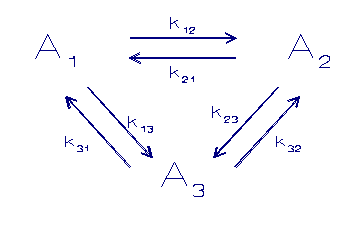
Een ander model gaat uit van een competitie tussen substraten
zoals dat door Morel (1983) gepostuleerd wordt:
A = component in oplossing
B,C = component in een vaste fase
k = sorptie snelheidconstanten
De adsorptie plaatsen staan in competitie met elkaar volgens
een kinetisch model. De verschillende sorptie sites zijn in
staat direct uit te wisselen met de oplossing. Zodoende krijgt
men een competitie systeem uitgedrukt in de grootte van de
adsorptie constanten.
Men kan zo'n systeem zien als een oppervlakte gecomplexeerd
model waar bepaalde plaatsen van het substraat sterker
gebonden zijn dan andere.
5.3.2. Analytische oplossing
Alle kinetische modellen kunnen opgelost worden door de
differentiaal vergelijkingen op te stellen en de
randvoorwaarden
in te vullen. Indien de beginvoorwaarden bekend zijn, is het
model compleet gedefinieerd. Het model wordt gedomineerd door
de adsorptie snelheidsconstantes (k-waarden).
Bovenstaande modellen konden opgelost worden door een algemeen
model dat beschreven staat in Bamford en Tipper (1969). Het
kinetische model bestaat uit:
Integratie van de differentiaal vergelijkingen, welke de
verandering van de concentratie in de tijd beschrijven, leidt
tot onderstaande oplossingen:

waarin:
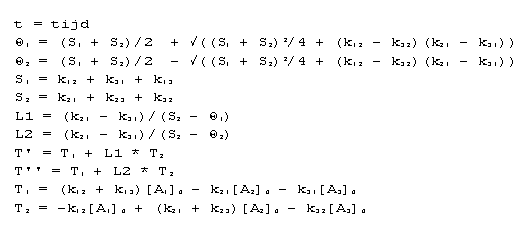
De modellen zoals die in het voorafgaande beschreven zijn
kunnen uitgedrukt worden als deze exacte oplossing door in de
algemene oplossing de juiste parameters te substitueren.
De modellen worden opgebouwd door de beginvoorwaarden
(beginconcentratie) [A1-3]0 te definiëren en de sorptie
snelheids-
constanten k's te kiezen. De sorptie snelheidsconstanten kan
men aanpassen.
5.3.3. Numerieke oplossing
De beschrijvingen
van de modellen
zijn hier als illustratie gegeven
de experimentele
gegevens zijn
daarbij in de grafiek geplaatst. De
afname van A1 in
het model van Bamford and Tipper
(1969) komt overeen met de opgeloste concentratie
van zink in oplossing. Een voorbeeld van eerste
orde verdwijning
(k13=1.3) wordt gegeven in figuur 1.

Figuur 1. Model beschrijving m.b.v. eerste orde adsorptie.
Er is getracht om
de experimentele
gegevens zo goed
mogelijk te fitten met een k12-waarde. Het blijkt dat met dit
model alleen de eerste paar uur een goede fit geven, de
concentratie van A1 neemt continu af totdat snel een
concentratie
van 0 wordt bereikt. In het volgende model wordt een k21
gebruikt waardoor na zekere tijd een evenwicht toestand wordt
bereikt. Dit is weergegeven in figuur 2.
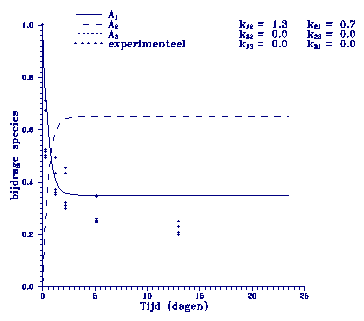
Figuur 2. Model beschrijving m.b.v. een eerste orde adsorptie reactie-snelheidsconstante k12.
De experimentele
gegevens blijken aan dit model te voldoen gedurende enkele
uren.
Het model komt dan op een bepaald constant niveau terwijl in
de experimenten de
concentratie afneemt. Ook dit
model benadert de
werkelijkheid dus
niet.
Een doorgeefmodel
is weergegeven in
figuur 3.

Figuur 3. Model beschrijving m.b.v. opeenvolgende eerste orde adsorptie reacties.
Het
model wordt in
eerste instantie
gedomineerd door
de sorptie snelheidsconstanten k12
en k21, gevolgd
door relatief
langzame sorptie,
met een constante
k23 die op den duur
dominant wordt.
Als laatste model
staat geïllustreerd in figuur
4.
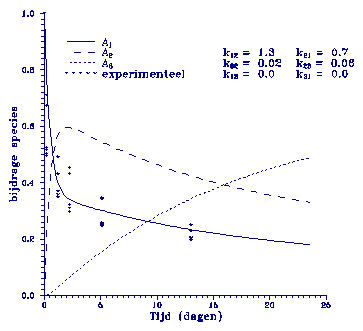
Figuur 4. Model beschrijving m.b.v. opeenvolgende eerste orde reacties met reversibele
sorptiesnelconstanten.
Het model is
opgebouwd door
vier sorptie snelheidconstanten. Dit betekent dat het systeem na verloop van
tijd in evenwicht komt. Het blijkt de experimentele
sorptiecurve redelijk goed te beschrijven, maar het nadeel is
dat men
hier vier onbekende k-waardes voor nodig heeft terwijl dat in
het vorige model opgebouwd werd door slechts drie. De modellen
kunnen het experimentele gedrag redelijk verklaren. Met name
de laatste twee lijken dit redelijk te doen.
Hoewel vroeger gebruik moest worden gemaakt van analytische
oplossingen omdat men niet in staat was berekeningen snel uit
te voeren wordt tegenwoordig gebruik gemaakt van de de computer
om differentiaal vergelijkingen nummeriek op te lossen.
We hebben hierbij o.a. gebruik gemaakt van het
modelleringsprogramma Frame. De in het model gebruikte
differentiaalvergelijkingen ingevoerd worden en het model kan
berekend
worden en gecalibreerd. De calibratie d.w.z. het afschatten
van de k-waardes, tot de beste fit bereikt is, kan indien men
een analytische oplossing heeft ook met het statische pakket
Systat (Wilkinson, 1988). Maar dit heeft zijn beperkingen
indien de oplossingen te
uitgebreid werden.
Frame bleek in
onze modellen geschikt te zijn voor
zeer uiteenlopende
kinetische modellen.
5.3.4. Calibratie
Calibratie van de
k-waardes kan
plaatsvinden aan
de hand van een
eenvoudig trial en
error methode. Men
kan de gemeten
waarden vergelijken d.m.v. een
model indien de
exacte oplossing
bekend is. Dit
lijkt een slechte methode maar uit ervaring weet men hoe de
grafiek moet verlopen in de concentratie gebied waar geen
waarden voor zijn. Door de parameters (k-waarden) te
veranderen krijgt men een indruk hoe aan welke grenzen de
k-waardes
mogen of kunnen voldoen. Bij een systeem waar de k-waardes
sterk kunnen varieren en toch de curve kunnen fitten, heeft
men met een sterk elastisch model te maken, de betrouwbaarheid
voor een k-waardes wordt dan klein. Calibratie met behulp van
de computerprogramma is ook mogelijk we hebben daartoe het
Nonlin programma van Systat (Wilkinson, 1988) gebruikt. Systat
vereist een analytische oplossing en heeft daarom zijn
beperkingen en dit verkleint zijn mogelijkheden. Het programma
vergelijkt de analytische oplossing met de gemeten waarden en
maakt het kwadraat van de afwijking zo klein
mogelijk.(kleinste kwadraten methode). Het bleek dat het
programma voor
eenvoudige modellen toepasbaar was maar indien de oplossing
zeer uitgebreid was lukt dit met Systat niet meer.
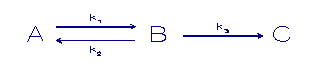
Voor de calibratie van k-waardes kan men uitgaaan van bepaalde
principes. Zo kan men de waardes constant nemen door
bijvoorbeeld gedurende de eerste tijd ( 2 dagen )
enkelvoudige 1e
orde sorptie reacties te veronderstellen, dit betekent dat in
een bovenstaand model, k1 en k2 eerst geschat worden en "vast"
gezet en vervolgens k3 schatten. Dit betekent dat het model
minder "elastisch" wordt en tot betere resultaten kan leiden.
Calibratie met Frame werkte voor onze modellen goed. Het
voordeel van Frame is dat het uiteenlopende problemen aankan
en zeer flexibel is.
5.4. Conclusie
Het blijkt dat de
adsorptie proeven
zoals die bij zink
uitgevoerd zijn
verklaard kunnen
worden met kinetische modellen en
dat een goede fit
verkregen kan worden. Een nadeel
bleek dat het niet
gemakkelijk is om
de resultaten
zoals die bij de
sorptie proeven
gevonden zijn te
gebruiken bij kinetische studies.
Omdat men betrouwbare sorptiesnelheids constanten
wil moet men relatief vaak bemonsteren. Men moet voor dit doel
een optimale bemonsteringsschema
opstellen.
Men kan ook stellen dat als men speciaal de kinetiek wil
bestuderen daarbij specifieke experimenten moet opstellen. Het
is daarbij wenselijk om de concentratie in tussenliggende
fasen te kunnen meten. Dit is mogelijk indien bijvoorbeeld de
concentratie in de waterfase constant wordt gehouden. Men zal
dan telkens een hoeveelheid metaal moeten toevoegen. Een
verfijning van het kinetische onderzoek betekent ook een
verfijning van de experimenten. Op aanvraag is een
gecompileerd FRAME programma (geen copyrechten verschuldigd)
verkrijgbaar van het drie compartimenten model.
5.5. Referenties
Bamford C.H. and Tipper C.F.H. (1969) Chemical kinetics.
Amsterdam, Elsevier Publ. Comp. p 486
Frame (Friendly Applied Modelling Environment). Remedy Systems
Modelling, Enschede, 1990
Wilkinson, Leland. SYSTAT: The system for statistics.
Evenston, Il: Systat, Inc. 1988



Titel rapport: